Diaper Economics Details and Derivation

By BitterGrey

For the sake of brevity and readability, the article "Diaper Econ" had three limitations. You might be reading this because of one of them (or you enjoy kinky academic pursuits.) First, it couldn't go into details about the various benefit and cost factors that drive the curves. Second, it didn't cover some notable options, such as not wetting the diapers or wearing cloth. These pros, cons, and options of being in diapers are detailed elsewhere. Third, it didn't show the steps and assumptions of the derivation itself. This article will try to cover this third limitation.

Derivation

First, let's start with some assumptions. One simplification we can't make is that supply and demand can reorder independently. They could in Adam Smith's case, but not ours. In the classical example, someone who was willing to spend $5 on a widget could go to any supplier until he found one for $5 or less. We can't do that here. If you want the benefits that come from wearing diapers to school, you'll have to accept the costs of wearing diapers to school. Without the ability to reorder customers and suppliers, the supply and demand curves become more complicated. These curves will be determined by an individual's costs and values, including the factors detailed above and more.

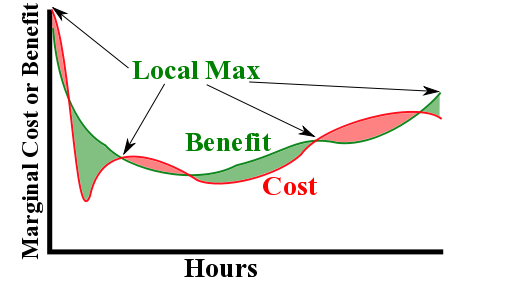
One decision we'll make is to explore the situation of an experienced ABDL at steady state. He'd have adjusted his practices so that costs are minimized, enjoyment is maximized, and that transients such as habituation are compensated for. This is a necessary approximation, since it gives us two functional curves. Without it, we'd need to consider transients, options, etc. Additionally, we'll assume both curves are continuous. Effectively, this involves assuming that the costs and benefits of, for example, wearing 20 hours per week isn't that different from wearing 20 hours, 1 minute per week. Together, these assumptions and approximations give us two functional curves. We've simplified things down to the case shown in the figure below. This figure represents arbitrary costs and values. The curves for any particular ABDL will differ, as will the most 'profitable' point.

For discussion's sake, we'll call this particular ABDL Max. He's a paraphilic infantilist, as is clear from the value spike and cost (binge-and-purge) near zero percent. (These benefit and cost factors are detailed in pros, cons, and options of being in diapers.) He wants to wear 24/7 so he'd be able to experiment with incontinence, or at least be passably incontinent among coworkers.

The profit, for lack of a better word, is simply the benefit minus the cost. Since the figure shows the marginal benefits and costs, the profit would also be marginal. If the marginal benefit for the 20th hour per week was $5/hr, and the marginal cost $3/hr, the marginal profit would be $2/hr. This marginal profit can be either positive or negative. The total profit for any duration will then be sum of all the marginal profits up to that duration. This is the integral of the profit curve. In the above figure, the total profit would be the green area minus the red area, up to the amount worn.

Visually, we know we'd want to include as much green area as possible, while including as little red area as possible. Calculus tells us that the total profit would have local minimums or local maximums at the ends of the curve, as well at points were the marginal profit is zero.

The leftmost limit, where diapers are almost never worn, is a local maximum for Max. Wearing diapers a little more would include more time with a negative marginal profit. This would be a change from bad to worse for Max: He'd be binging and purging more. Similarly, the rightmost limit, wearing 24/7, is a local maximum for Max. That is, he'd profit from wearings diapers all the time more than he would wearing them nearly all the time.

In addition to the two end limits, there are local maximums or minimums everywhere the curves cross. ( Where the marginal benefit and marginal cost curves cross, the marginal profit is zero.) Fortunately for Max, there are only five of these. Max's first crossing is a local minimum, wearing diapers around 5% of the time. For Max, this would involve rapid and deep binging and purging. He'd get that leftmost patch of red, an area of negative profit, and nothing else. The next crossing is a local maximum, at around 15%. At this level, he'd be wearing for the unprofitable 5% but also the profitable time between 5% and 15%. This might have Max scratching his head, since this is close to where his shy bladder gives him the most marginal trouble. Similarly, Max would have a second local minimum around 40%. At this point, he'd get the two leftmost red patches and only the leftmost green patch. That is, one area of profit and two areas of loss. There is also a local maximum at around 65%, and another local minimum at around 95%.

Clearly, the most profitable point for Max, the global maximum, is one of the local maximums. For the curves shown, it is either 0%, 15%, 65%, or 100%. In this case, we have the luxury of knowing the curves. That first, leftmost green area is bigger than the first red area, so 15% is more profitable than 0%. Similarly, the second green area is larger than the second red area, so 65% is more profitable than 15%. However, the third green area is not larger than the third red area, so 100% (24/7) is not more profitable than 65%. Thus, while Max might want to go 24/7, the benefits don't outweigh the costs.

While you might be a lot like Max, you aren't him. Most importantly, you probably don't have your cost and value curves plotted out. However, like him, your global maximum will also be a local maximum, which means it is either one of the limits or a point where the curves cross. Without knowing the curves, you can find a local max by starting at some level, maybe 2%, 5%, or 10%. At that level, if marginal benefits outweigh marginal costs, you are in a green area, so wear a little more. If marginal benefits are less than marginal costs, you are in a red area, so wear a little less. Continue doing so until the benefits and costs balance each other out. That will be a local maximum. (If they balance out at your starting point, try a different point. That might be either a local maximum or a local minimum.) This approach, Adam smith's "invisible hand," is sufficient to find a local maximum without knowing the curve.

An important thing to keep in mind is that, at this local maximum, you should want to wear diapers more. At that point, your marginal benefit (how much you want to wear diapers) should be equal to or greater than the marginal cost. Since cost is generally greater than zero, your benefit should also be greater than zero. You should want to wear diapers more... even if you are in them 24/7. Otherwise, you're wearing them too much.

This local maximum might or might not be your global maximum. To look for better maximums, try a different starting point; the 'second hand' described in Diaper Econ. Increasing the number of starting points you've tried will increase your odds of finding the global maximum. It will also give you a better understanding of your own benefits and costs, in case you want to sketch out your own curves.

Do you have Questions, tips, suggestions, or other feedback?

Related Topics: A non-ABDL artists blog on his Ten Days in Diapers